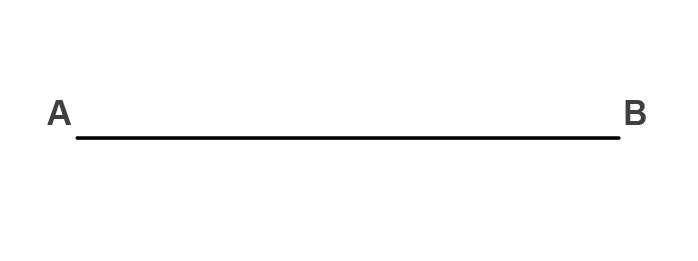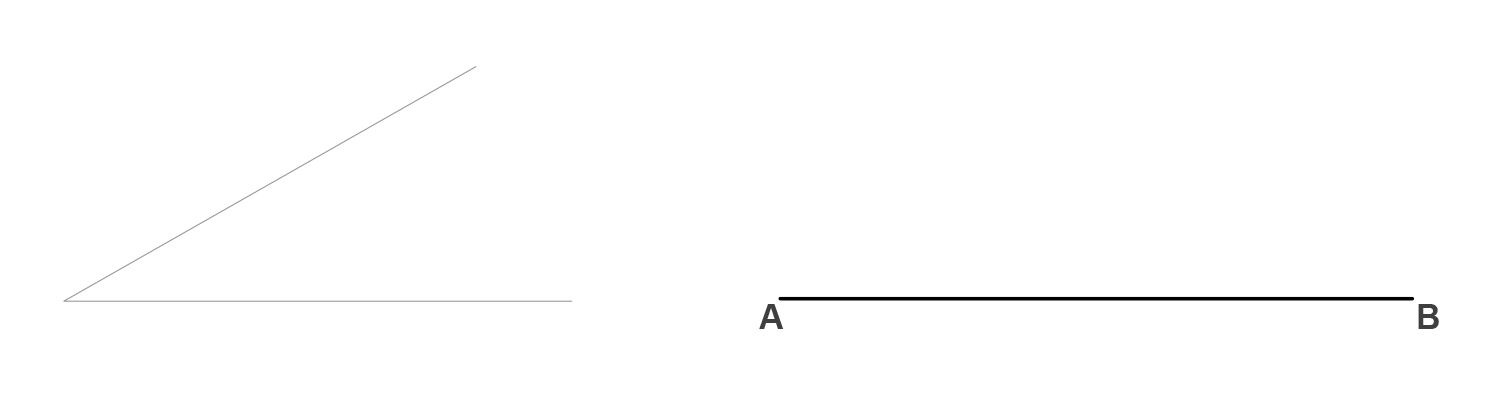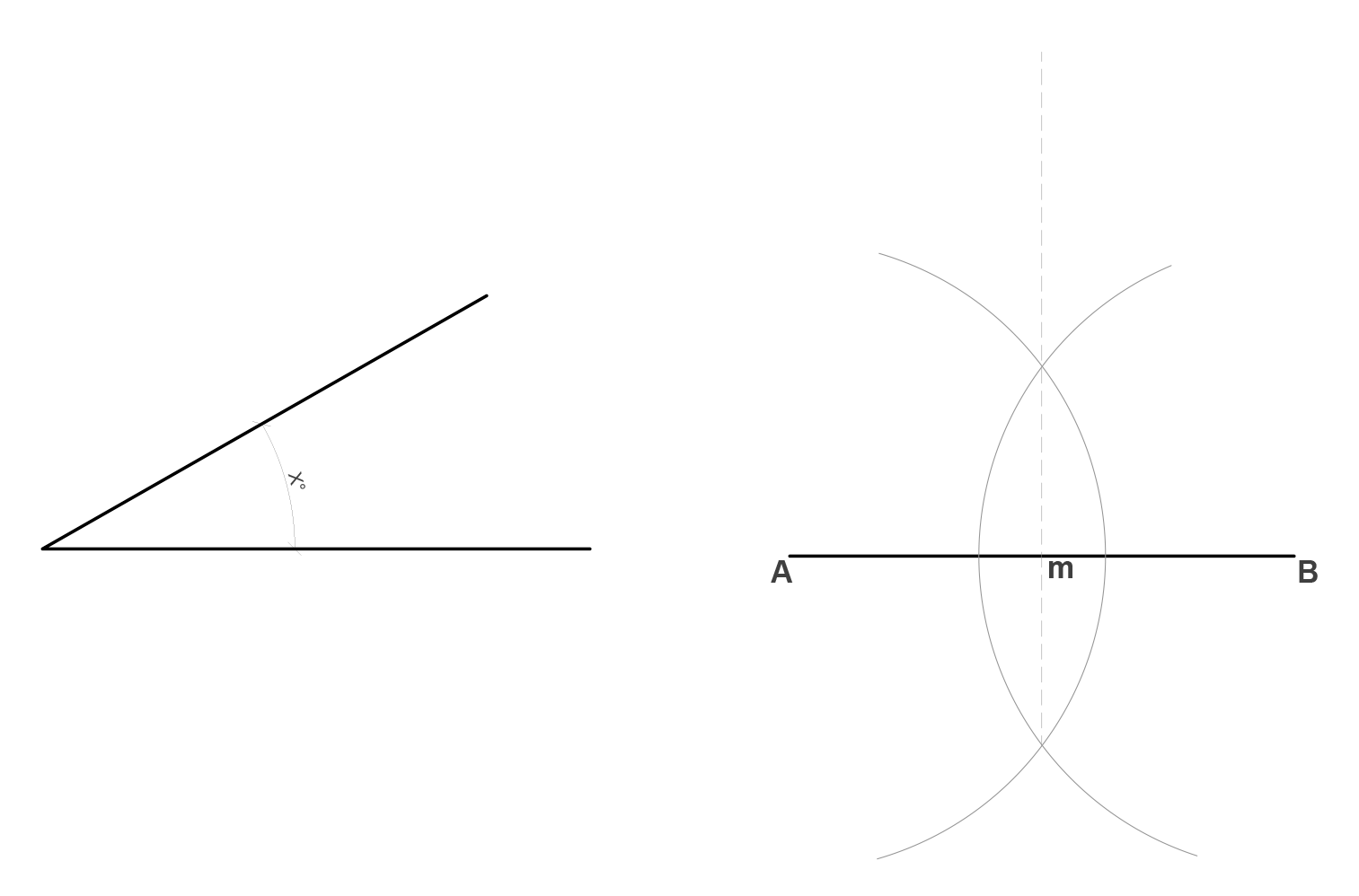En este nuevo apunte de dibujo realizaremos mediante instrumentos los trazados geométricos básicos que debemos dominar al iniciar el dibujo técnico de cualquier pieza, vista o proyecto de forma manual aunque también es válido para el dibujo en AutoCAD y/o práctica. Este tipo de trazados básicos son la clave para desarrollar trazos más complejos como tangencias y enlaces.
Las operaciones principales que realizaremos en esta primera parte del apunte son las siguientes:
1) Dividir un segmento en “N” partes iguales.
2) Copiar un ángulo.
3) Simetral o mediatriz de un segmento.
4) Bisectriz de un ángulo.
5) Perpendicularidad a partir de un punto conocido fuera del segmento.
6) Perpendicularidad en un punto cualquiera dentro de un segmento.
7) Paralelismo (recta paralela a otra), con o sin distancia asignada.
8) Arco capaz de un ángulo.
1) Dividir un segmento en partes iguales
La operación consiste en dividir de forma geométrica un segmento en “N” partes iguales sin necesidad de hacer cálculo alguno, no importando el largo o tamaño del segmento.
Sea el segmento AB dado:
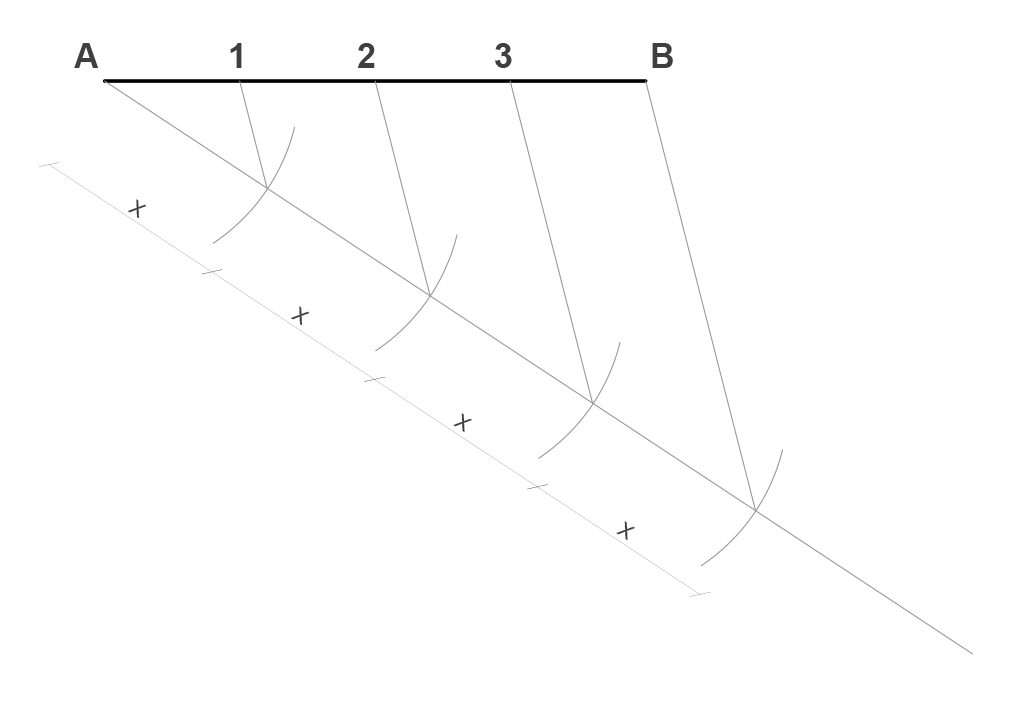
Tomando como inicio el punto A, dibujaremos una recta de medida N (ampliable) en un ángulo cualquiera, de preferencia no tan cerca o “pegado” respecto del segmento AB (30° a 45° es lo recomendable).
Realizamos un arco de círculo tomando como centro el punto A de un radio X arbitrario.
Tomando como centro la intersección entre el arco y la recta, repetimos el mismo radio las veces que queramos dividir el segmento (en el ejemplo es 4).
Tomando el último punto de intersección entre el arco y la recta dibujaremos un segmento entre esta y el otro extremo del segmento AB (punto B).
Finalmente, realizamos rectas paralelas a la línea recién creada que pasen por la intersección entre cada arco y recta formando así los puntos 1, 2 y 3; y terminando la división del segmento.
2) Copiar un ángulo a un trazo o segmento
La operación consiste en hacer una copia fiel de un ángulo dado a un trazo o segmento ya establecido.
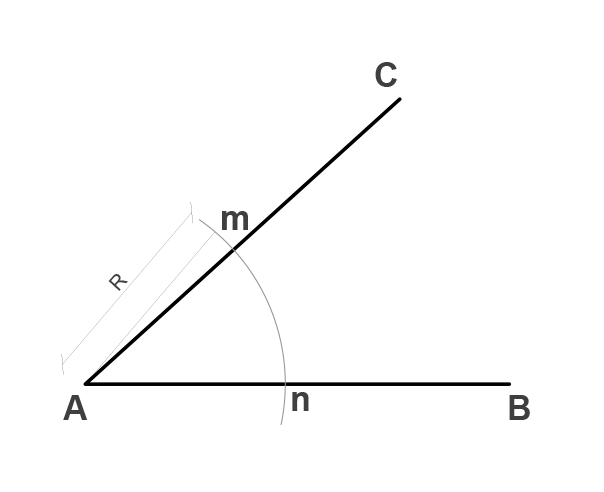
Sea un ángulo y el segmento AB dados:
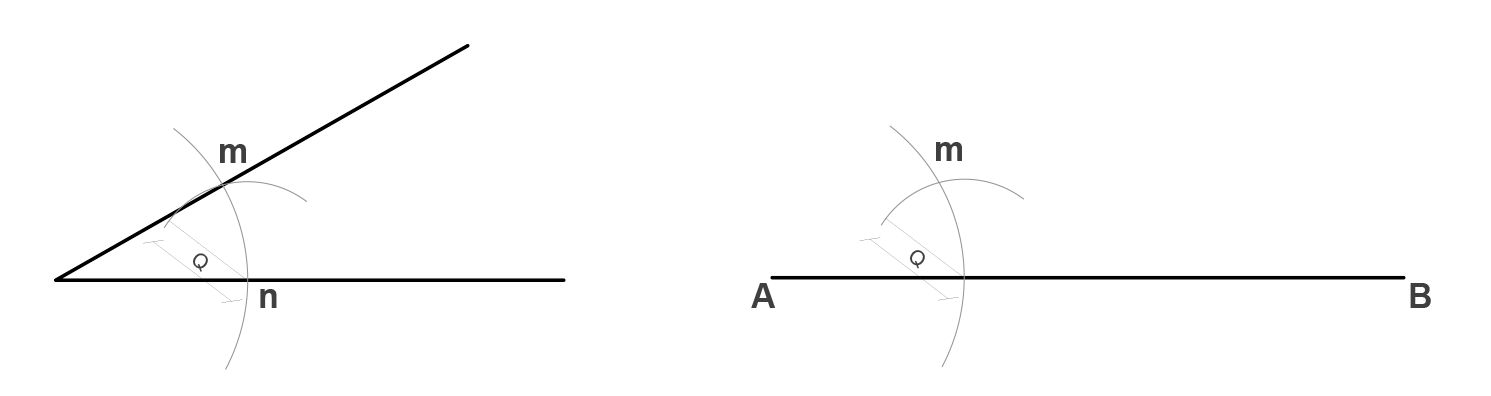
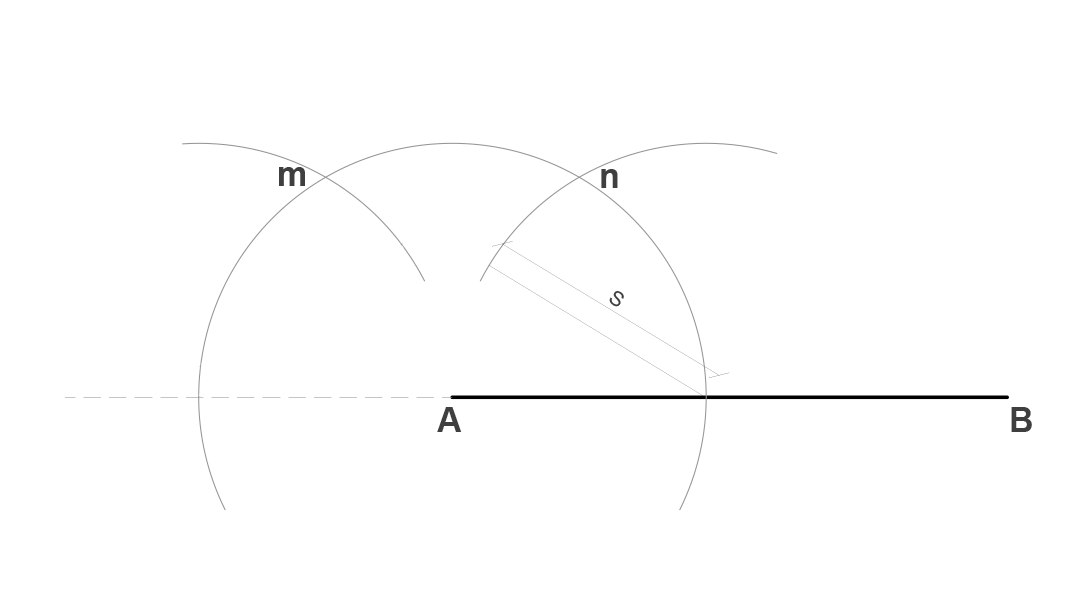
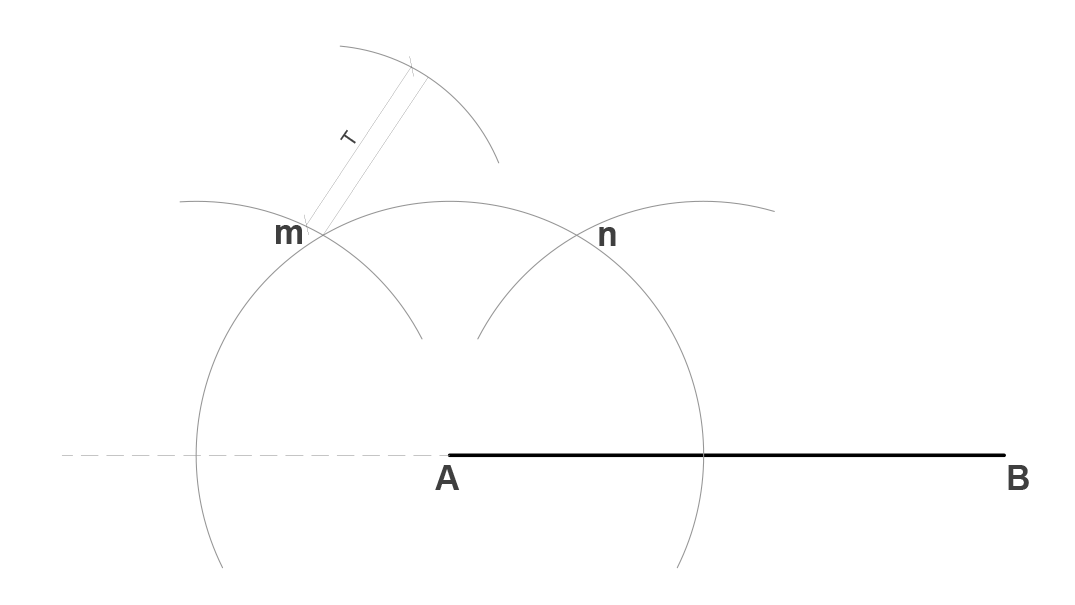
Tomando como centro el inicio del ángulo generamos un arco de círculo de magnitud R de tal modo que intersecte a ambas rectas. Realizamos el mismo arco en el segmento tomando como centro el punto A. Se forman los puntos m y n en el ángulo.
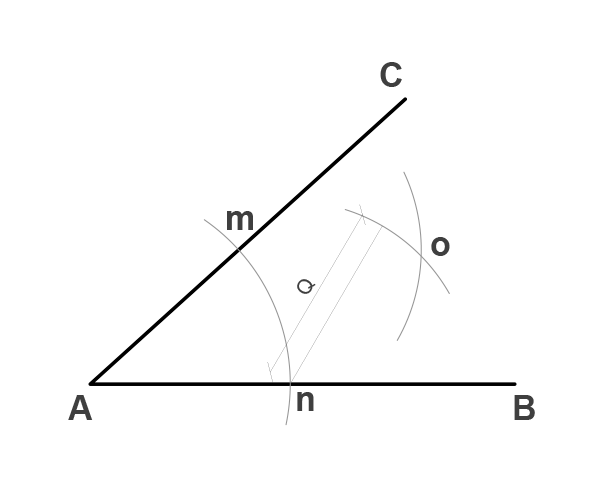
Tomando como radio los puntos m y n (Q), realizamos un arco en el segmento AB tomando como centro la intersección entre el arco y el segmento. Con esto obtenemos el punto m.
Finalmente unimos el punto A con el punto m formado en el segmento AB, y ya tenemos el ángulo copiado.
3) Generar la mediatriz (simetral) de un segmento
La operación consiste en encontrar de forma geométrica el trazo perpendicular que a su vez marca el punto medio o la mitad de un trazo o segmento.
Sea el segmento AB dado:
Tomando como centro el punto A, realizamos un arco de círculo de tal modo que a simple vista sea mayor que la mitad del segmento, con un radio R arbitrario.
Repetimos el mismo proceso pero esta vez tomando como centro el punto B. Obtenemos los puntos c y d.
Finalmente unimos los puntos c y d para obtener la simetral o mediatriz y el punto m, que es la mitad del segmento.
4) Generar la bisectriz o bisectar un ángulo
La operación consiste en dividir de forma geométrica un ángulo dado en dos mitades, es decir, dos ángulos de igual medida que sumados nos dan el ángulo inicial.
Sea el ángulo ABC dado:
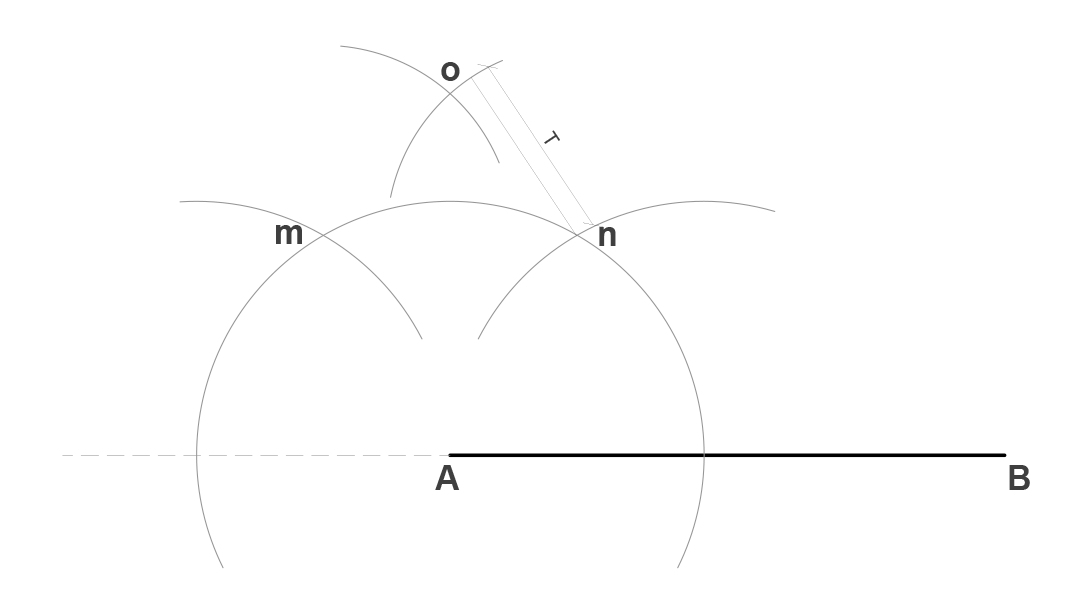
Tomando como centro el punto A, generamos un arco de círculo de magnitud R (arbitraria), de tal modo que intersecte a ambas rectas AC y AB. Obtenemos los puntos m y n en el ángulo.
Tomando como centro el punto m, generamos un arco de círculo de magnitud Q (arbitraria) de tal modo que ocupe el mayor espacio interno posible del ángulo o que intersecte a este. Obviamente, también podemos usar el primer radio (R) para realizar este procedimiento.
Repetimos el mismo proceso, pero esta vez tomando como centro el punto n. Obtenemos el punto o.
Finalmente unimos los puntos A y o para obtener la bisectriz pedida.
5) Generar la perpendicular de un segmento que pase por un punto conocido fuera de este
La operación consiste en generar de forma geométrica una línea perpendicular al segmento y que a su vez pasa por un punto ya conocido fuera de este.
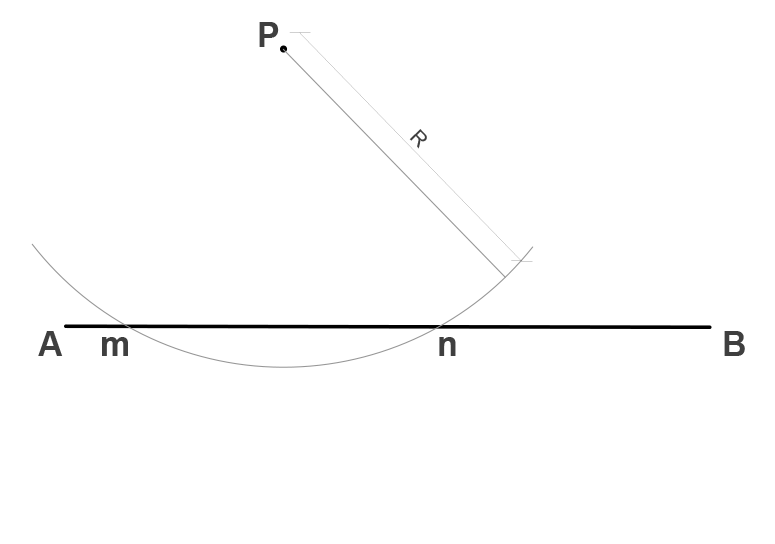
Sean el segmento AB y el punto P dados:
Tomando como centro el punto P y con un radio R dado, generamos un arco de tal modo que este intersecte con el segmento, formando los puntos m y n.
Tomando como centro el punto m y con un radio S de tal modo que este sea a simple vista mayor que la mitad del trazo mn, generamos un arco de circunferencia.
Repetimos el proceso pero esta vez tomamos el punto n como centro, obteniendo el punto t.
Finalmente unimos los puntos t y P para obtener la perpendicular pedida.
6) Generar la perpendicular a un punto cualquiera dentro de un segmento
La operación consiste en generar de forma geométrica una línea perpendicular al segmento y que a su vez pase por cualquier punto dentro de este, sin necesidad de un punto externo.
Sea el segmento AB dado:
En este caso, generaremos la perpendicular en el punto A. Por ello, proyectamos el trazo AB hacia la izquierda de este.
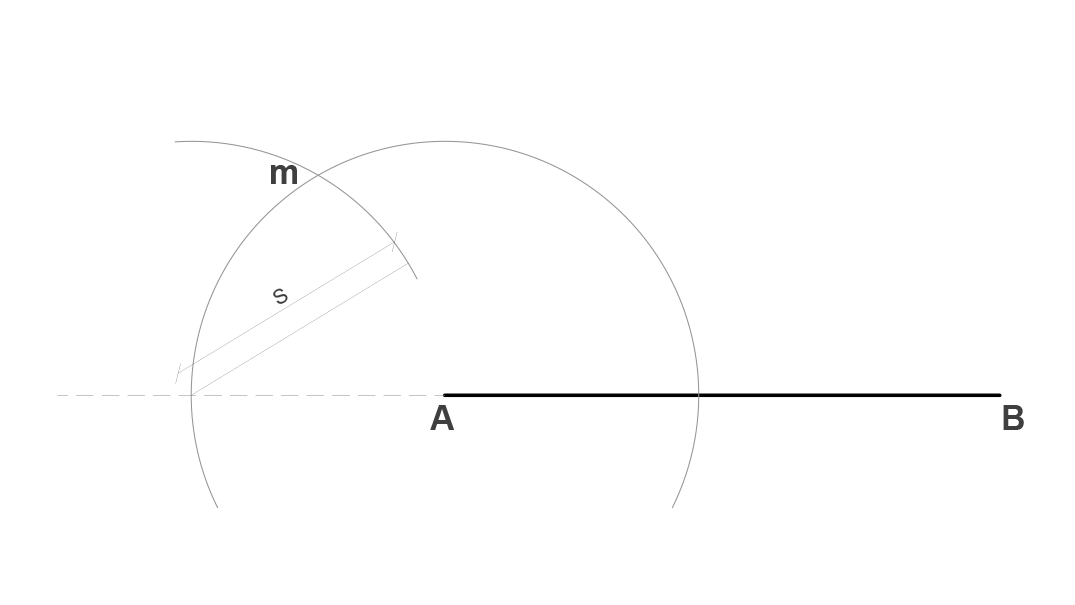
Tomamos como centro el punto A y con un radio R dado, generamos una semicircunferencia de tal modo que esta intersecte entre las rectas.
Ahora tomamos como centro la primera intersección entre la proyección del trazo AB y el arco, y con un radio S dado generamos un arco para obtener el punto m.
Repetimos el proceso pero esta vez tomamos la otra intersección como centro, obteniendo el punto n.
Ahora tomamos como centro el punto m y con un radio T de tal modo que este sea mayor a la mitad del trazo mn, generamos un arco de circunferencia.
Repetimos el proceso pero esta vez tomamos el punto n como centro, obteniendo el punto o.
Finalmente unimos los puntos o y A para obtener la perpendicular pedida.
7) Generar la paralela a un segmento o recta
a) generar la paralela sin una distancia específica:
La operación consiste en generar de forma geométrica una línea paralela al segmento o la recta dada.
Sea el segmento AB dado:
Tomamos un punto cualquiera del segmento (puede ser el centro, por ejemplo) y desde allí generamos una semicircunferencia de tal modo que esta intersecte con el segmento, formando los puntos m y n.
Tomando como centro el punto m y con un radio S definido, definimos un arco de tal forma que intersecte al semicírculo ya creado, obteniendo el punto t.
Repetimos el proceso pero esta vez tomamos el punto n como centro, obteniendo el punto u.
Finalmente trazamos una línea entre los puntos t y u formando la línea paralela pedida. En este caso la distancia perpendicular entre ambas no es el radio S sino que es un valor un poco menor que este.
b) generar la paralela asignando una distancia perpendicular específica entre ellas:
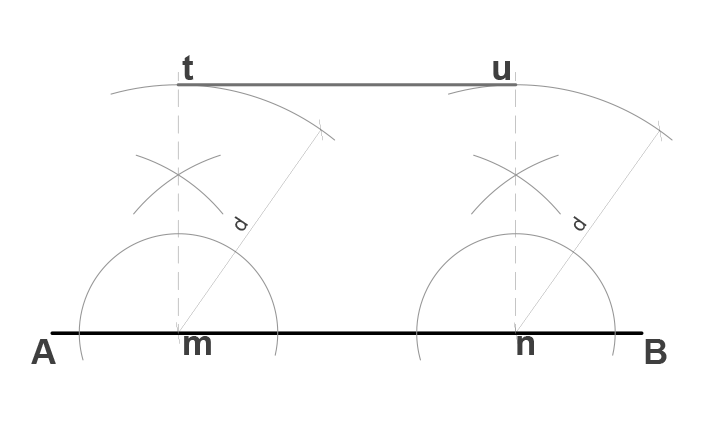
En este caso lo que haremos primero será realizar las perpendiculares en dos puntos cualquiera dentro del segmento (puntos m y n). Una vez obtenida la recta, debemos proyectarla hacia arriba.
Luego definimos un radio arbitrario (d), el cual será la distancia que asignaremos entre las líneas paralelas. Tomando como centro los puntos m y n y usando el radio d, realizamos arcos de circunferencia de tal modo que cada uno de estos intersecte a la recta perpendicular proyectada, formando los puntos de intersección t y u.
Unimos los puntos t y u y con ello obtenemos la paralela pedida, esta vez con una distancia perpendicular d asignada entre ellas.
8) Generar el arco capaz de un ángulo
La operación consiste en generar de forma geométrica un arco en el cual todos sus ángulos proyectados desde los extremos del segmento que lo contiene tengan el mismo valor del ángulo inicial. El arco capaz se define como el lugar geométrico de los vértices de los ángulos que tienen la misma amplitud y abarcan un mismo segmento.
Sean un ángulo de X° y un segmento AB dados:
Primeramente, realizaremos la simetral del trazo AB para obtener el punto m y posteriormente proyectaremos la perpendicular obtenida hacia arriba.
En el trazo copiaremos el ángulo Xº de tal forma que nos quede debajo del trazo AB con elpunto A como inicio de este.
Ahora generaremos la perpendicular en el ángulo Xº de tal forma que la proyección de la perpendicular se intersecte con la vertical de la simetral del segmento AB, obteniendo el punto o.
Finalmente, tomando como centro el punto o y con radio Ao, dibujamos un arco de circunferencia que intersecta a los puntos A y B. Este es el arco capaz del ángulo Xº pedido.
Podemos comprobar esto trazando ángulos hacia cualquiera de los puntos de este arco y tomando los puntos A y B como extremos de este, donde notamos que el valor de todos es Xº.
Otras relaciones importantes
Elementos notables de un triángulo:
Alturas: son los segmentos perpendiculares que van desde un vértice hacia el lado opuesto de este. Las alturas confluyen en un punto llamado Ortocentro (h) el cual puede estar dentro, coincidir con un vértice o fuera del triángulo según el tipo de triángulo.
De esto mismo podemos concluir que el Ortocentro (h) será externo en triángulos obtusángulos, coincidirá con el vértice del ángulo recto en caso de un triángulo rectángulo, y será interno si el triángulo es acutángulo.
Bisectriz: son las bisectrices de cada uno de los ángulos internos del triángulo. Las bisectrices confluyen en un punto llamado Incentro (I) el cual a su vez es el centro de la circunferencia que se inscribe en el interior del triángulo (circunferencia inscrita).
Por lógica el incentro (I) siempre está en el interior de triángulo, independiente de su tipo.
Simetral: son las simetrales o mediatrices de cada uno de los lados del triángulo. Las simetrales confluyen en un punto llamado Circuncentro (o) el cual a su vez es el centro de la circunferencia que se circunscribe en el exterior del triángulo y por ende, está a igual distancia de cada vértice (circunferencia circunscrita).
El circuncentro puede estar dentro o fuera del triángulo según el tipo o forma de este.
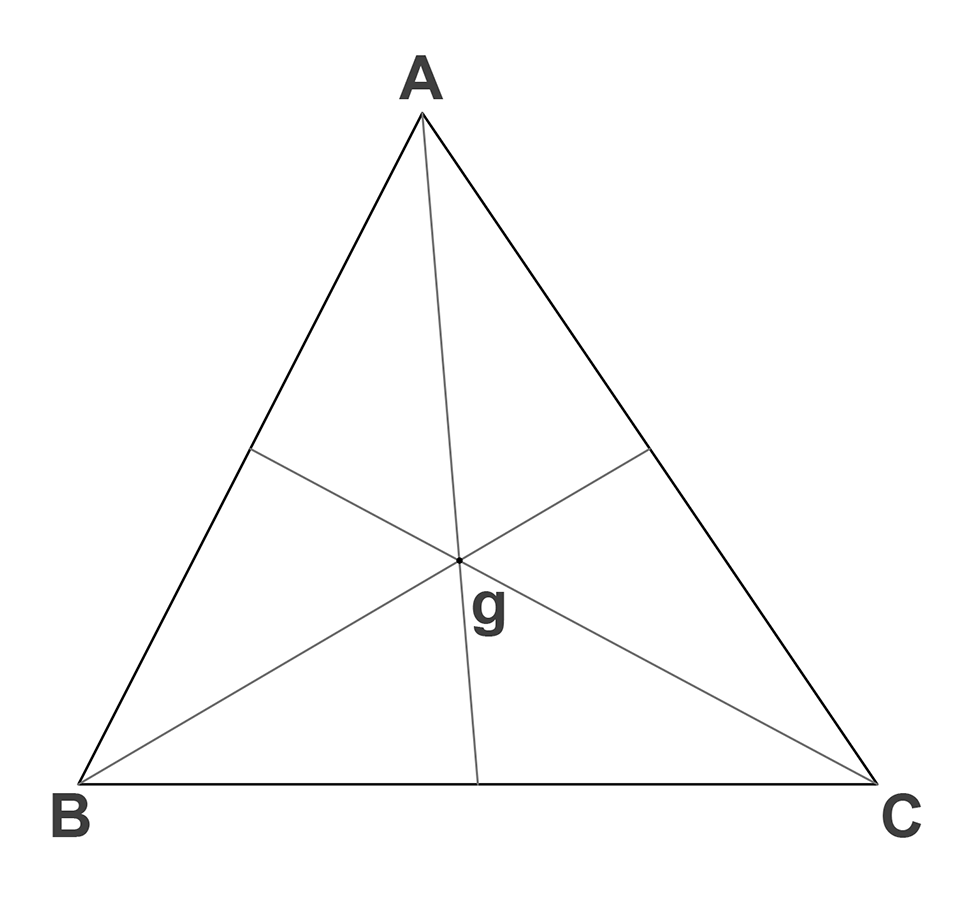
Medianas: son los segmentos que van desde un vértice hacia el punto medio del lado opuesto de este. Las medianas confluyen en un punto llamado Baricentro o centro de gravedad (g).
La mediana divide el triángulo en dos triángulos más pequeños pero que tienen la misma área. En cada mediana, la distancia entre el baricentro y su punto de origen es 2/3 de la longitud total de la mediana respecto a la distancia entre el baricentro y el lado opuesto, que es el 1/3 restante.
En un segundo y tercer apunte veremos trazos más complejos como tangencias y enlaces de líneas y curvas.