En este apunte veremos el comando de AutoCAD llamado circle, el cual como su nombre lo indica nos permitirá definir y dibujar círculos de forma fácil y rápida posicionándolos en cualquier parte del espacio de trabajo. Los círculos se podrán dibujar de varias maneras posibles aunque la más tradicional es definirlo según su centro y su radio. Además, tendremos la ventaja que esta forma se convierte en un objeto unificado una vez dibujado.
El comando circle
Circle es un comando que nos permitirá dibujar un círculo en 2D desde un punto específico y en cualquier posición. Lo podemos invocar realizando clic en su icono correspondiente:
O también escribiendo circle (o su abreviatura c) en la barra de comandos y luego presionando la tecla enter:
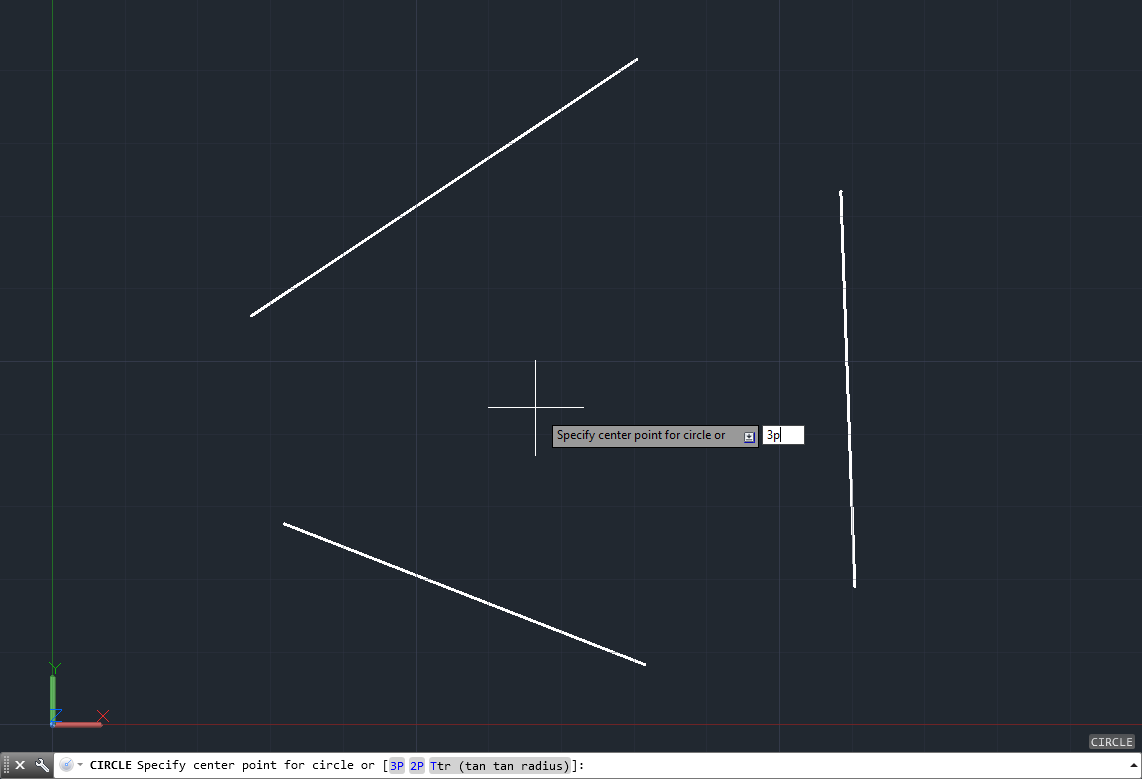
Al invocar a circle, la barra de comandos nos mostrará varios métodos de dibujo y por defecto nos pedirá que ingresemos el primer punto del centro del círculo a dibujar:
Podremos definir ese punto mediante un clic en el espacio de trabajo o también mediante coordenadas (X,Y) y luego presionando enter, siempre y cuando en este último caso tengamos desactivada la entrada dinámica (F12). Una vez que lo hacemos, arrastraremos el mouse para “definir” la magnitud del radio ya que el siguiente clic que realicemos será para definir el punto final de este, y con ello ya tendremos el círculo dibujado:
Al realizar el clic final el círculo se define y el comando se cierra. La magnitud del radio la podremos definir mediante el método anteriormente descrito o bien, si queremos una magnitud específica, ingresamos el valor de esta y presionamos enter, justo después de haber definido el punto central:
En el ejemplo se ha definido el radio del círculo en 3, lo hacemos escribiendo la magnitud y luego presionando enter luego de definir el centro.
Sin embargo, si volvemos a invocar el comando, al definir el punto central del círculo encontramos la siguiente opción:
- Diameter (D): nos permite definir la magnitud del diámetro del círculo en lugar de su radio. Al ingresar al subcomando, nos pedirá el valor numérico de este. Lo podemos definir mediante un valor numérico y luego presionando enter o, de manera similar a radius, mediante un clic en un punto específico del espacio.
Debemos recordar que Diameter = 2Radius, por lo tanto habrá una gran diferencia de tamaño según elijamos la opción Radius o Diameter en la definición de nuestro círculo:
En el ejemplo el primer círculo posee radio=4 mientras que el segundo posee un diámetro del mismo valor, y notamos claramente que el segundo círculo es la mitad de tamaño que el primero.
Ahora bien, si invocamos el comando circle y aún no definimos el centro de nuestro círculo, la barra de comandos nos mostrará metodologías nuevas para el dibujo de círculos que son las siguientes:
Estas mismas metodologías de dibujo también pueden ser previsualizadas si hacemos clic en la flecha inferior del icono de circle:
Estas metodologías son:
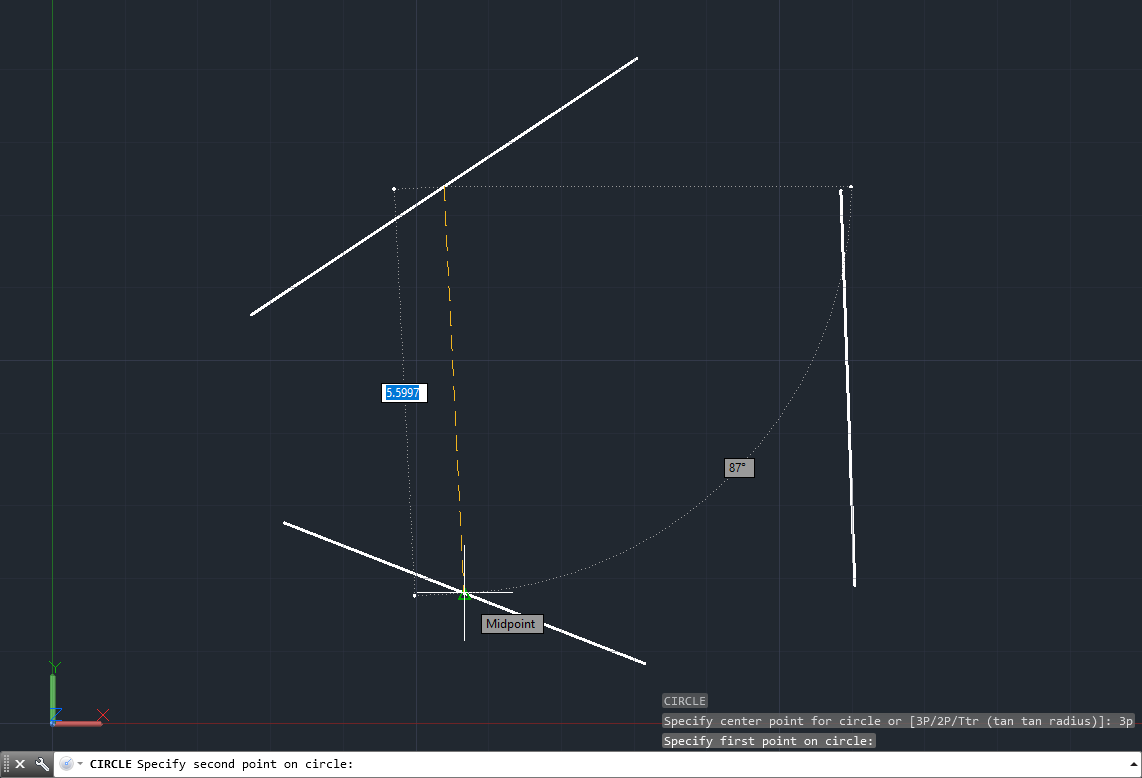
- 3P (3 puntos): nos permitirá definir el círculo según 3 puntos específicos. En este caso, al activar la opción la barra de comandos se nos indicará ingresar el primer punto, lo ingresamos mediante clic en la pantalla o mediante coordenadas (X,Y), luego nos pedirá los siguientes dos y procedemos de la misma forma para definir el círculo:
En el ejemplo se toman como puntos los tres midpoints de las rectas para definir el círculo mediante la metodología 3P.
Debemos tomar en cuenta que este método sólo establece la definición de tres puntos los cuales son parte del perímetro del círculo, y en ningún caso implican tangencia o alguna otra relación geométrica a las referencias.
- 2P (2 puntos): nos permitirá definir el diámetro del círculo según 2 puntos específicos. En este caso al activar la opción la barra de comandos nos indicará ingresar el primer punto, lo ingresamos mediante clic en la pantalla o mediante coordenadas (X,Y), luego nos pedirá el siguiente y procedemos de la misma forma para definir el círculo:
En el ejemplo se toman como puntos los dos midpoints de las rectas para definir el cìrculo mediante la metodología 2P.
Debemos tomar en cuenta que este método sólo establece los dos puntos los cuales son parte del perímetro del círculo y en ningún caso implican tangencia o alguna otra relación geométrica a las referencias.
- Ttr (Tan Tan Radius): nos permitirá definir el círculo según 2 puntos específicos (los cuales serán tangentes a las referencias tomadas) y luego el radio entre estas. En este caso, al activar la opción la barra de comandos nos indicará seleccionar la primera tangente, la cual puede ser cualquier punto del espacio o de la referencia. La ingresamos mediante clic en la pantalla o mediante coordenadas (X,Y), y luego nos pedirá la siguiente:
Una vez definidas nuestras tangentes, la barra de comandos nos pedirá el radio comprendido entre estas pero por defecto, nos mostrará el radio actual entre las tangentes seleccionadas:
Si no hacemos nada y sólo presionamos enter, el círculo se definirá con este radio y respetará la posición de los puntos tangentes definidos antes:
Podemos resumir esta metodología en el esquema siguiente, donde vemos el radio del círculo definido mediante el radio de las tangentes por defecto y cómo el círculo se define entre las rectas de referencia:
Sin embargo, si cambiamos el radio y definimos una magnitud mediante un valor numérico y luego presionando enter, los puntos serán diferentes a los ya tomados pero seguirán siendo tangentes a las referencias:
En el ejemplo se define una magnitud de 4 y los puntos se desplazan, aunque siguen siendo tangentes a las líneas de referencia.
como ya sabemos, al presionar la flecha que está debajo del icono circle poseemos las opciones ya vistas anteriormente y, además, se nos agrega una nueva opción llamada Tan, Tan, Tan la cual nos permitirá definir el círculo mediante tres puntos los cuales serán tangentes a la referencia.
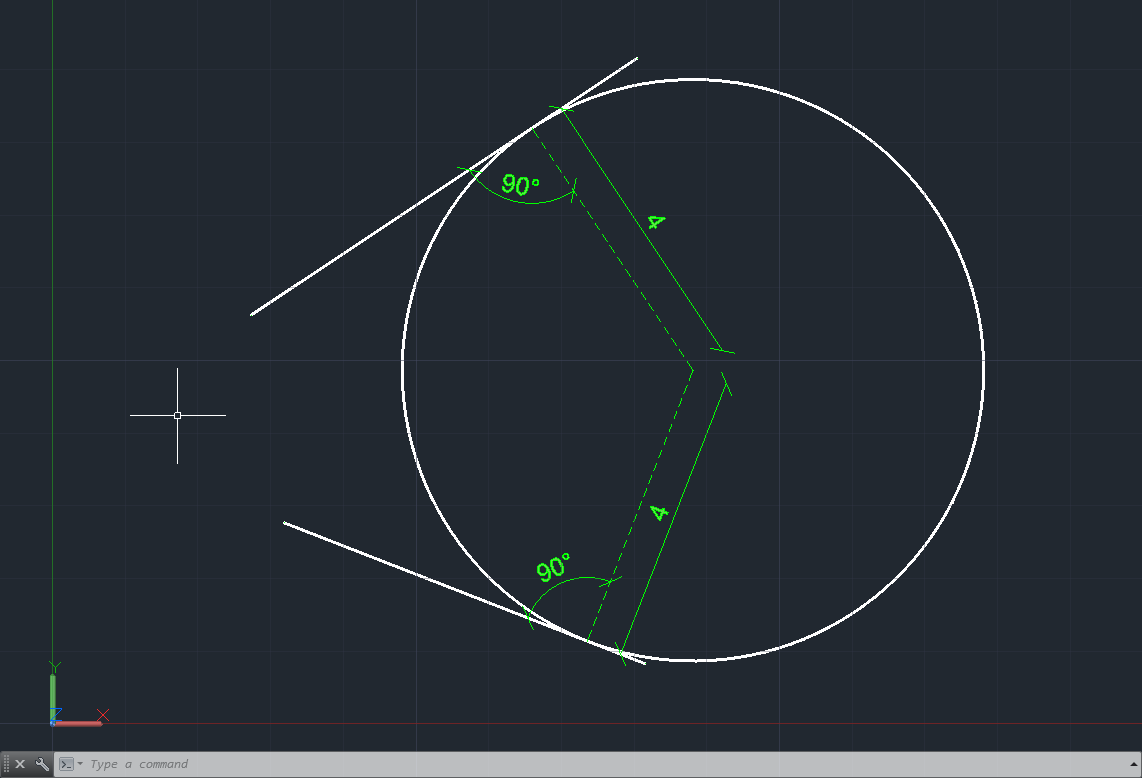
En este caso elegimos Tan, Tan, Tan y luego elegiremos tres puntos los cuales serán las tangentes del círculo dibujado, aunque en este caso en particular no podremos definir el radio del círculo pues este se definirá sólo por las tres tangentes:
En el ejemplo se definen mediante Tan, Tan, Tan tres puntos (uno por cada recta) y el círculo dibujado es tangente a cada una de las rectas en su mismo punto.